In this week of CS50x we learned different Searching and Sorting Algorithms.

We started with two searching algorithms the Linear search and the Binary search.

Linear Search

In linear search we iterate through the data one element at a time using a loop and compare the current element with the element to find (say key). If we find the element we return it's position within the array. If we have iterated through the complete array and not found a match we simply return "Element not found".

Linear search has the simplest implementation, but it is only suitable for small data sizes as when dealing with large data sets the algorithm takes much longer to run.

We were thus introduced to the concept of running time or time complexity, the best case Ω (omega) i.e. lower bound, the worst case O (BigO) i.e. upper bound, and the average case Θ (theta) for the time required to execute the algorithm. These functions are evaluated based on the size of the problem v/s the time required

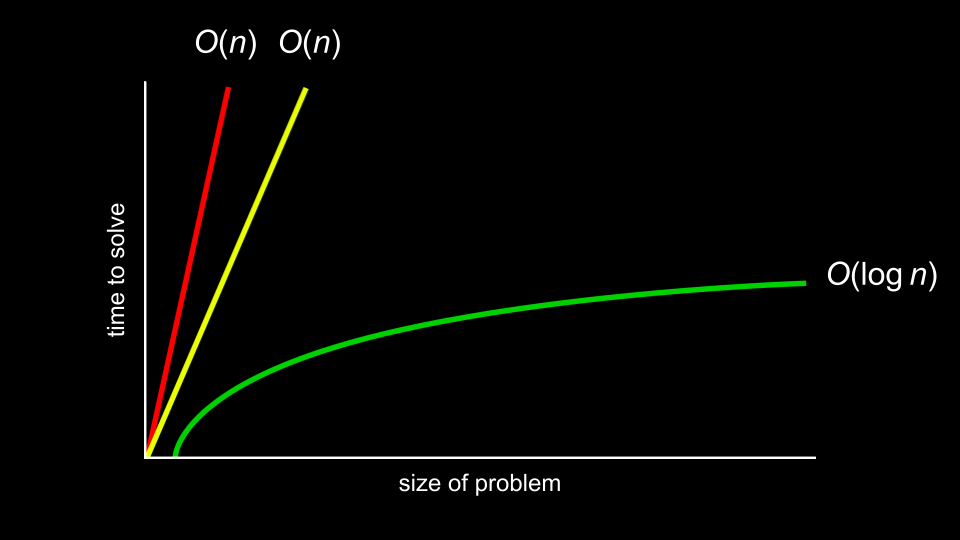
img credit: CS50

Linear Search has a time complexity of O (n) as in the worst case we would need to iterate through every element of the array.

Binary Search

In Binary search we recursively iterate through the array by finding the middle element and comparing it with the element to be found (key). To perform binary search on an array it's elements need to be sorted. We find the mid element by the arithmetic: mid = (low + high)/2 , where mid, low and high are index of middle first and last element of the array. If they are equal then the algorithms stops and returns the position of the element. If the key is greater than the mid element we consider the right part of the array by changing low = mid +1 and repeat the process, if the key is smaller than the miod element then we consider the left part of the array by high = mid - 1 and repeat this process until either we find the array or we run out of comparisions mathematically: low > high.

The time complexity of Binary Search is O (log n) or more precisely O (log2 n)because it would take exponenetially fewer steps in every iteration, specifically half the number of steps in every iteration. Thus Binary search is more efficient for a large data set.

Data Strucutres

We learned how to create user defined data structures in C using structs.

For example: to create a phonebook here is a data strucutre called person.

typedef struct
{
    string name;
    string number;
}
person;

Sorting Algorithms

Sorting the process of converting an unsorted list into a sorted list, i.e. in an ascending (or descending) order.

Selection Sort:

In Selection sort we go through every element in the array and choose the smallest element in the current iteration and swap it with the first element of the unsorted array, thus the smallest element in each iteration will get selected and sorted.

The time complexity of selection sort is: O (n^2)

Bubble Sort:

In Bubble sort we go through the array and compare every 2 adjacent elements and swapping them if the number with lower index is more than the one with higher index, such that in every iteration we move the highest number to the end of the array. Thus simulating a bubble that floats it's way to the surface, hence the name Bubble sort. As we sort the aray after every iteration we can skip the sorted end of the array and only focus on the unsorted part of the array.

Time complexity for Bubble sort is: Best case: Ω (n) and Worst case: O (n^2).

Merge Sort:

Recursion: It is a process where a function calls itself during it's execution. During recursion we must have a base case that allows the function to avoid infinite recursion where in the function to call itself infinitely. It is very useful to implement a loop without needing to use an iterative strucutre such as a for or while loop.

We can use recursion to implement the merge sort algorithm, the pesudocode for merge sort is:

If only one number
    Quit
Else
    Sort left half of number
    Sort right half of number
    Merge sorted halves

Thus in merge sort we recursively divide the array into smaller halves and end up with 2 elments which can then be compared and sorted and then when we merge the 2 halves we can make sure they are sorted. Thus with the help of recursion we can operate on a large data set efficiently.

Time complexity of merge sort is O (n log⁡ n) for the worst case, it is still Ω (n log⁡ n) for the best case as the algorithm must visit every element in the array, thus the time complexity of merge sort is Θ (n log⁡ n).

Problem Set:

In the problem set for this week there were 3 assignments:

1. Sort: Different files and 3 program were provided and the task was to determine the sorting algorithms that were present in each program, it was challenging but using time complexities I could figure out the solution.

2. Plurality: The task was to implement an election system in C where the candidate with the highest votes wins the election. It ivolved using structs to define a special structer and using different function to reach the solution.

3. Runoff: The task was to implement a runoff election system in C using the knowledge gained until now. It was very challenging because the task was to implemnt 6 functions. The implementation of each function wasn't too difficult but the whole program was very overwhelming to understand and implement, but by focussing on one function at a time I managed to solve the problem and implement the required program. It was a fun and challenging journey!